El algoritmo consiste formalmente en los siguientes pasos:
- Inicialización de todos los nodos con distancia "infinita", iniciar el nodo de comienzo con 0.
- Marcar las distancias del nodo inicial como permanentes, todas las demás como temporales.
- Establecer el nodo inicial como activo.
- Cálculo de las distancias temporales de todos los nodos vecinos a el nodo activo sumando sus distancias con los pesos de los arcos.
- Si la distancia calculada de un nodo es menor a la actual, actualiza la distancia y fija el nodo actual como antecesor, Este paso es llamado actualización y es la idea central de Dijkstra.
- Estableciendo el nodo con la distancia temporal mínima como activa, marca sus distancia como permanente.
- Repita los pasos del 4 al 7 hasta que no queden nodos con una distancia permanente cuyos vecinos tengan aún distancias temporales.
Siguiendo estos pasos, se presenta la versión "naive" del algoritmo de Dijkstra implementado en R y con ayuda de los paquetes "igraph" y "viridis"
library(igraph)
library(viridis)
#############################################################################
# Dijkstra
Dij = function(Graph, fuente){
dist = c() # VECTOR DE DISTANCIAS
source = fuente # NODO FUENTE
vertex = as.numeric(V(Graph)) # NODOS
previous = c() # NODO PREVIO
alt = c()
for (i in 1:length(vertex)){# INICIALIZACIÓN
# DISTANCIA INICIAL DESDE LA FUENTE HASTA EL VERTICE V
# SE ESTABLECE COMO INFINITO
dist[i] = Inf
# NODO PREVIO EN RUTA ÓPTIMA DESDE LA FUENTE
previous[i] = NA
}
# DISTANCIA DESDE LA FUENTE HACIA LA FUENTE
dist[source] = 0
# EL CONJUNTO DE TODOS LOS NODOS Q EN EL GRAFO
# TODOS LOS NODOS EN EL GRAFO NO ESTÁN OPTIMIZADOS
Q = vertex
# CICLO PRINCIPAL DEL ALGORITMO
while(length(Q)>0){
# NODO EN Q CON LA MENOR DISTANCIA
u = Q[which(dist[Q] == min(dist[Q]))][1]
# REMOVER u DEL CONJUNTO Q
Q = Q[-(which(Q==u))]
# HALLAR VECINOS DE u
vecino = as.numeric(neighbors(g, u))
# PARA CADA VECINO v DE u (DONDE v NO HA SIDO REMOVIDO DE Q)
for (i in 1:length(vecino)){
# CÁLCULO DE DISTANCIAS
alt[i] = dist[u] +
distances(g, v=u, to=vecino[i])
# ACTUALIZO DISTANCIA (u,v)
if (alt[i] < dist[vecino[i]]){
dist[vecino[i]] = alt[i]
# OBTENGO EL NODO PREVIO
previous[vecino[i]] = u
}
}
}
# BASE DE RESULTADOS
result = data.frame(Desde=LETTERS[fuente], Hasta=LETTERS[vertex],
Distancia=dist, Predecesor=LETTERS[previous])
# RECONSTRUCCIÓN DE RUTAS ÓPTIMAS
# DESDE LA MATRIZ CON LAS DISTANCIAS ÓPTIMAS
ruta = function(DIST, destino){
fuente = as.character(DIST[1,1])# NODO FUENTE
path = destino # NODO DESTINO
# MIENTRAS LOS NODOS SEAN DIFERENTES
# BUSCA LOS NODOS PREVIOS
# RECONSTRUYE LA RUTA ÓPTIMA
# ACTUALIZA EL NUEVO DESTINO
# FORMATO DE SALIDA DE LA RUTA
while(destino != fuente){
previo = as.character(DIST[which(DIST[,2]==destino),4])
path = c(previo, path)
destino = previo
path = paste(path, collapse = ' -> ')
}
return(path)
}
# APLICO FUNCIÓN DE RECONSTRUCCIÓN DE RUTAS ÓPTIMAS
# PARA TODOS LOS NODOS EN EL GRAFO
rutas = list() # INICIALIZO LISTA P/RUTAS
for (i in 1:nrow(result)){
rutas[[i]] = ruta(result, as.character(result[i,2]))
}
result$Rutas = unlist(rutas)
result = result[,-4]
return(result)
}
Se prueba el algoritmo en un grafo de 5 nodos:
# MATRIZ DEL GRAFO DE 5 NODOS
# > mat
# A B C D E
# A 0 4 0 2 0
# B 4 0 5 6 0
# C 0 5 0 7 1
# D 2 6 7 0 8
# E 0 0 1 8 0
# CREO GRAFO DESDE LA MATRIZ DE ADYACENCIA mat
# g = graph.adjacency(mat, weighted=TRUE)
# PLOTEAR GRAFO
# {set.seed(68); plot(g)}
El grosor de los arcos es proporcional a su "peso". La solución del grafo tomando como nodo inicial la letra "A" (fuente = 1) se produce con las siguientes líneas:
# APLICACIÓN DEL ALGORITMO CON NODO FUENTE "A" (EQUIVALENTE A 1)
# > Dij(Grafo=g, fuente=1)
# Desde Hasta Distancia Rutas
# 1 A A 0 A
# 2 A B 4 A -> B
# 3 A C 9 A -> D -> C
# 4 A D 2 A -> D
# 5 A E 10 A -> D -> E
Este resultado se puede verificar desde la matriz de adyacencia.
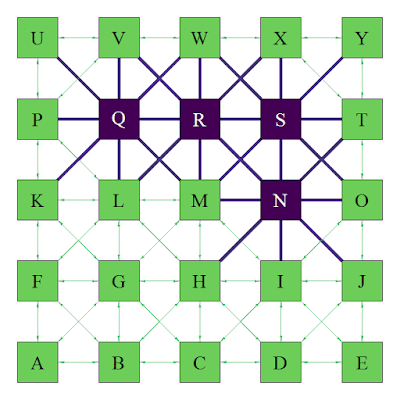

Gracias, favor incluir los pesos en grafo y el peso optimo desde hasta
ResponderBorrar